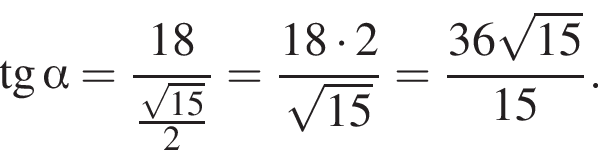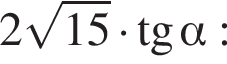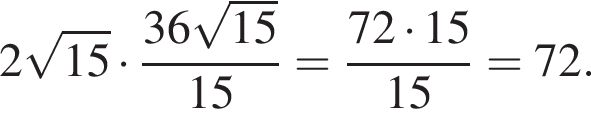На рисунках 1 и 2 изображены правильная треугольная призма ABCA1B1C1 и ее развертка. Найдите площадь боковой поверхности призмы, если длина ломаной ACA1 равна ![]() и точки A, C, A1 лежат на одной прямой (см. рис. 2).
и точки A, C, A1 лежат на одной прямой (см. рис. 2).
На рисунке изображен треугольник ABC, в котором ∠ACB = 38°, ∠AMN = 109°. Используя данные рисунка, найдите градусную меру угла BAC.
Используя рисунок, определите верное утверждение и укажите его номер.


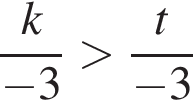
Среди чисел −7; −11; 11; −1; 0 укажите то, которое не меньше −9 и не больше −2.
Вычислите 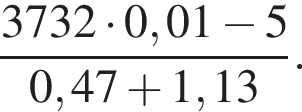
За n коробок конфет было заплачено 152 руб. 20 коп., а за n коробок печенья — b руб. Составьте выражение, которое определяет, на сколько копеек коробка печенья дешевле коробки конфет.
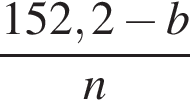
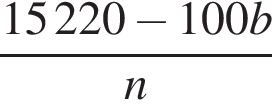
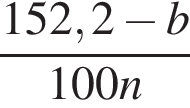
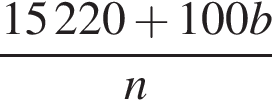
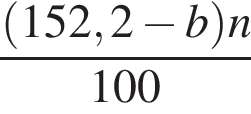
На рисунке a || b, 
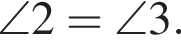 Найдите градусную меру угла 4.
Найдите градусную меру угла 4.
Найдите сумму всех целых значений функции y = f(x), заданной графиком на промежутке (-5; 5) (см.рис.).
Результат упрощения выражения 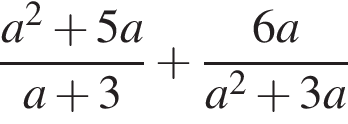 имеет вид:
имеет вид:
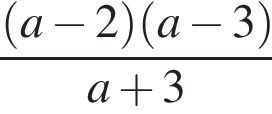
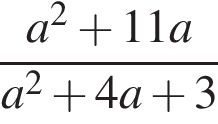
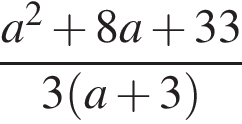
Найдите наибольшее натуральное двузначное число, которое при делении на 11 дает в остатке 7.
На диаграмме показано количество посещений сайта на протяжении недели (со вторника по воскресенье). Установите соответствие между вопросами А−В и ответами 1−6.
A) В какой день недели было на 20 посещений больше, чем в предыдущий?
Б) В какой день недели количество посещений было на 35% меньше, чем во вторник?
B) В какой день недели количество посещений было на 10% больше, чем в предыдущий?
1) Вторник
2) Среда
3) Четверг
4) Пятница
5) Суббота
6) Воскресенье
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения:
1) если 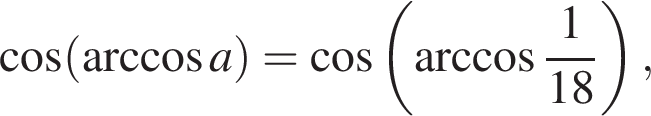 то
то 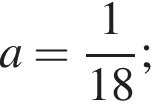
2) если 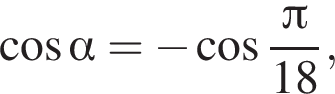 то
то 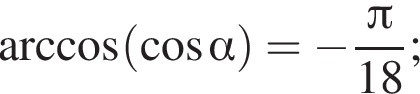
3) если 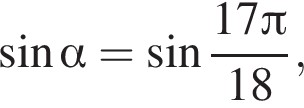 то
то 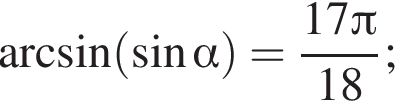
4) если 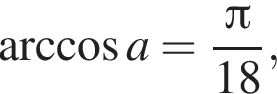 то
то 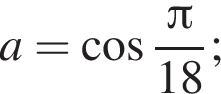
5) если 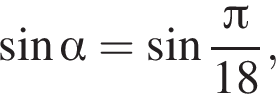 то
то 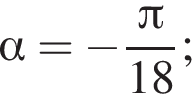
6) если 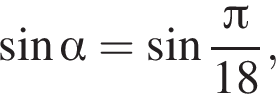 то
то 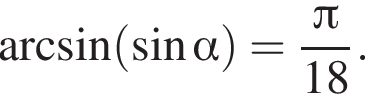
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Основание остроугольного равнобедренного треугольника равно 10, а синус противоположного основанию угла равен 0,6. Найдите площадь треугольника.
По углам прямоугольной пластины с периметром 448 см вырезали четыре одинаковых квадрата (см. рис.) с длиной стороны, равной 12 см. Края полученной заготовки загнули по линиям 1−4 и получили коробку в форме прямоугольного параллелепипеда объемом 48 дм3. Найдите площадь прямоугольной пластины (в дм2).
Найдите (в градусах) наименьший корень уравнения 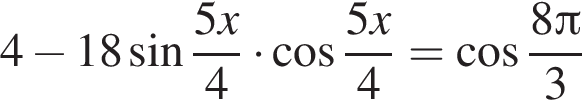 на промежутке (−180°; 0°).
на промежутке (−180°; 0°).
Площадь прямоугольника ABCD равна 20. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Найдите сумму всех целых решений неравенства 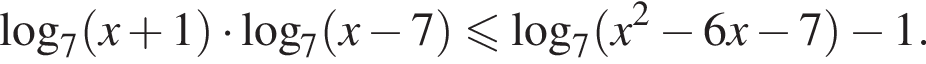
Найдите сумму квадратов корней уравнения 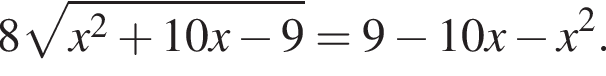
Найдите (в градусах) сумму корней уравнения 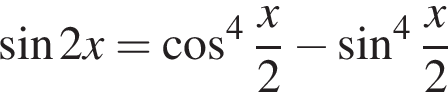 на промежутке [−223°; 333°].
на промежутке [−223°; 333°].
Из точки А проведены к окружности радиусом ![]() касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 5S.
касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 5S.
Двое рабочих выполняют некоторую работу. Сначала первый работал ![]() часть времени, за которое второй выполняет всю работу. Затем второй работал
часть времени, за которое второй выполняет всю работу. Затем второй работал ![]() часть времени, за которое первый закончил бы оставшуюся работу. Оба они выполнили только
часть времени, за которое первый закончил бы оставшуюся работу. Оба они выполнили только ![]() всей работы. Сколько часов потребуется рабочему с меньшей производительностью для выполнения этой работы, если известно, что при совместной работе они сделают ее за 3 ч 36 мин?
всей работы. Сколько часов потребуется рабочему с меньшей производительностью для выполнения этой работы, если известно, что при совместной работе они сделают ее за 3 ч 36 мин?
ABCDA1B1C1D1 — прямая четырехугольная призма, объем которой равен 960. Основанием призмы является параллелограмм ABCD. Точки M и N принадлежат ребрам A1D1 и С1D1, так что A1M : A1D1 = 1 : 2, D1N : NC1 = 2 : 1. Отрезки A1N и B1M пересекаются в точке K. Найдите объем пирамиды SB1KNC1, если 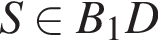 и B1S : SD = 3 : 1.
и B1S : SD = 3 : 1.
Отрезок BD является биссектрисой треугольника АВС, в котором 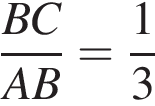 и
и 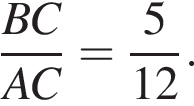 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
Основанием пирамиды SABCD является выпуклый четырехугольник ABCD, диагонали АС и BD которого перпендикулярны и пересекаются в точке O, АО = 9, ОС = 16, ВО = OD = 12. Вершина S пирамиды SABCD удалена на расстояние ![]() от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
от каждой из прямых AB, BC, СD и AD. Через середину высоты пирамиды SABCD параллельно ее основанию проведена секущая плоскость, которая делит пирамиду на две части. Найдите значение выражения 10 · V, где V — объем большей из частей.
Найдите сумму корней (корень, если он единственный) уравнения 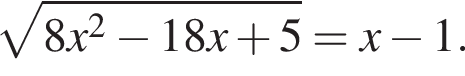 В ответ запишите полученный результат, увеличенный в 14 раз.
В ответ запишите полученный результат, увеличенный в 14 раз.
В большой круг шара вписан треугольник, длина одной из сторон которого равна 6, а противолежащий этой стороне угол равен 120°. Найдите значение выражения 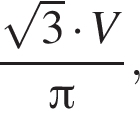 где V — объем шара.
где V — объем шара.
Найдите (в градусах) сумму различных корней уравнения 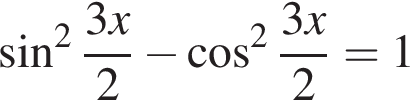 на промежутке
на промежутке 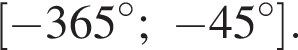
Найдите произведение корней уравнения 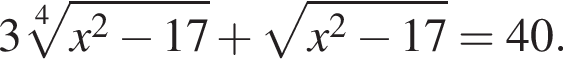
При делении некоторого натурального двузначного числа на сумму его цифр неполное частное равно 6, а остаток равен 7. Если цифры данного числа поменять местами и полученное число разделить на сумму его цифр, то неполное частное будет равно 4, а остаток будет равен 6. Найдите исходное число.
Основанием четырехугольной пирамиды является ромб, у которого косинус угла равен ![]() и длина стороны равна 8. Все боковые грани пирамиды наклонены к плоскости ее основания под углом α, а высота пирамиды равна 18. Найдите значение выражения
и длина стороны равна 8. Все боковые грани пирамиды наклонены к плоскости ее основания под углом α, а высота пирамиды равна 18. Найдите значение выражения 

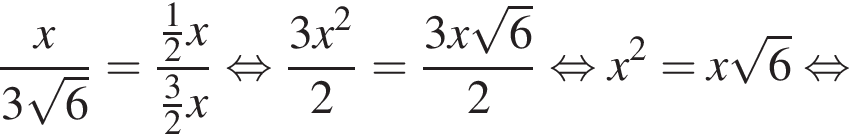
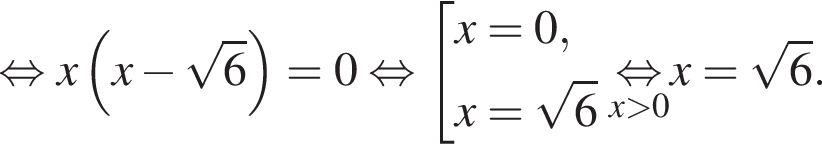
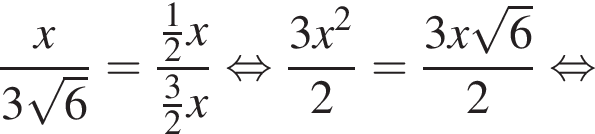
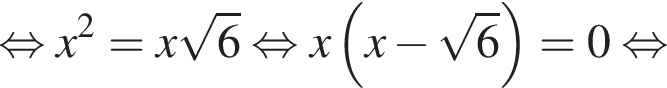
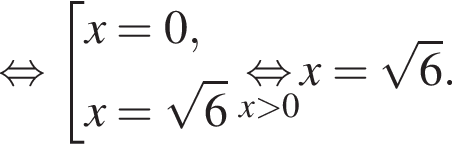
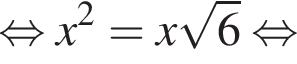
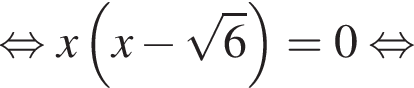
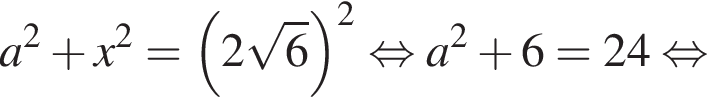

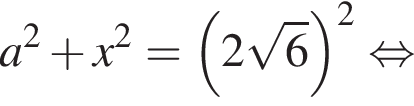
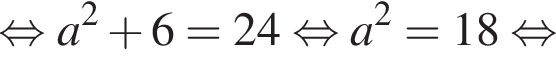
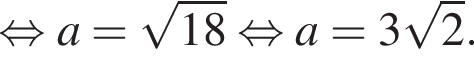
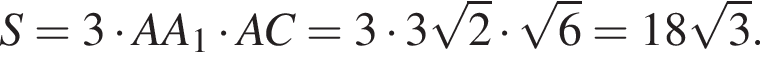
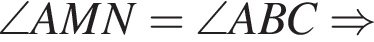
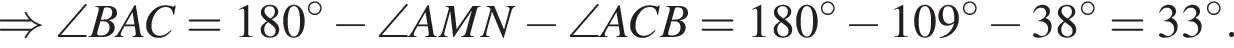
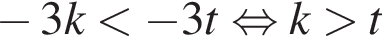 — неверно.
— неверно.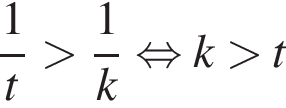 — неверно.
— неверно.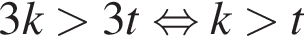 — неверно.
— неверно.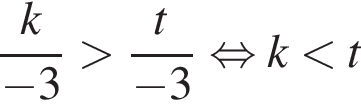 — верно.
— верно.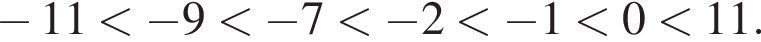
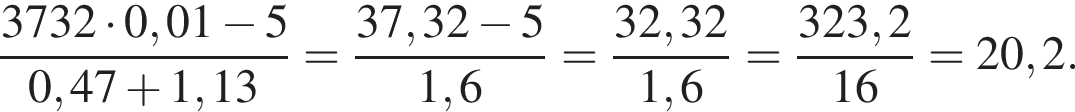
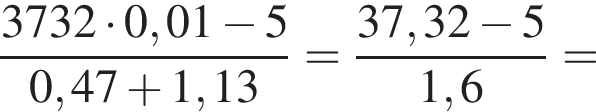
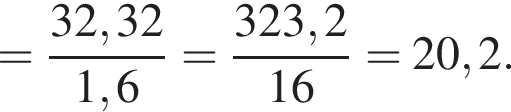
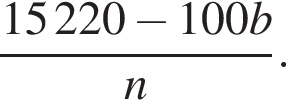
 Значит,
Значит, 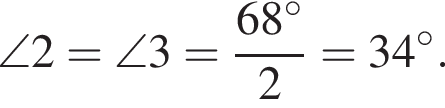 Тогда и
Тогда и 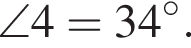
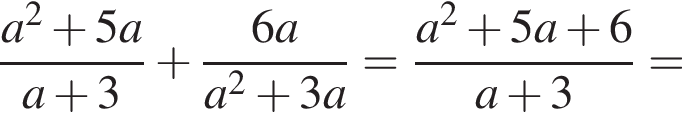
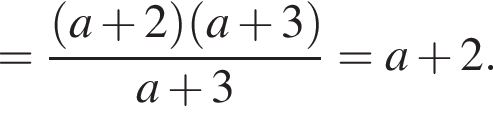
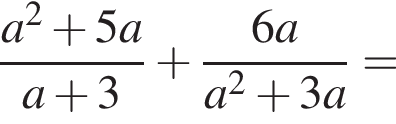
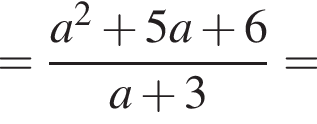
 Так как нужно найти наибольшее натуральное двузначное число, то a < 100. Решим неравенство:
Так как нужно найти наибольшее натуральное двузначное число, то a < 100. Решим неравенство: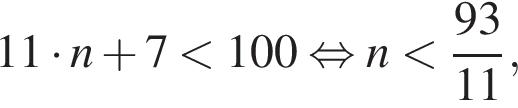
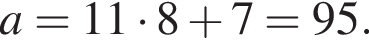
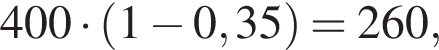 значит, количество посещений на 35% меньше, чем во вторник было в четверг (3).
значит, количество посещений на 35% меньше, чем во вторник было в четверг (3).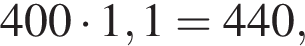 значит, в среду количество посещений было на 10% больше, чем в предыдущий (2).
значит, в среду количество посещений было на 10% больше, чем в предыдущий (2).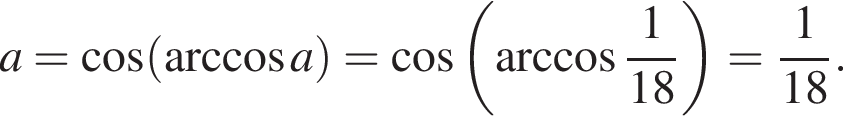

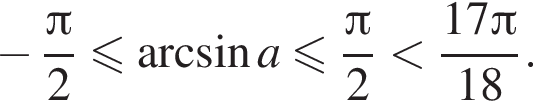
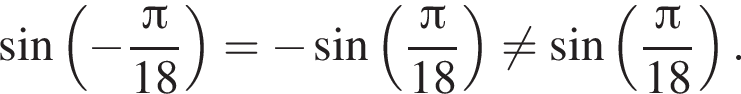
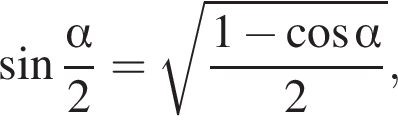 где
где 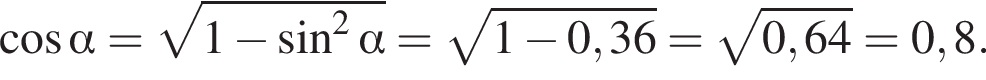
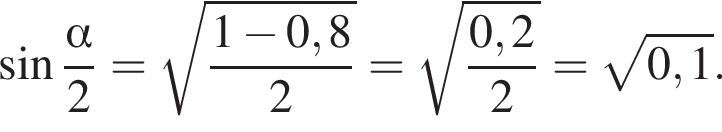
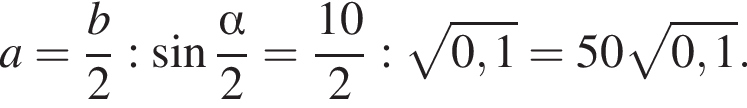 Тогда площадь треугольника равна:
Тогда площадь треугольника равна: 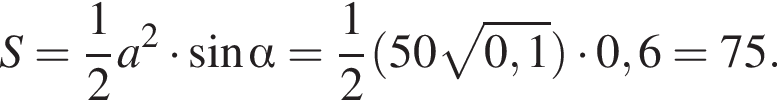
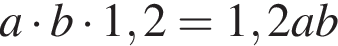 кубических дециметра, откуда
кубических дециметра, откуда 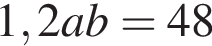 и
и 
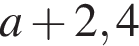 и
и 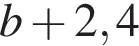 дециметра, поэтому периметр ее был равен
дециметра, поэтому периметр ее был равен 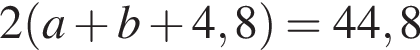 дециметра, откуда
дециметра, откуда 
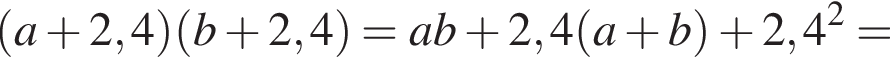
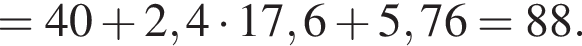
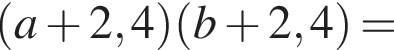
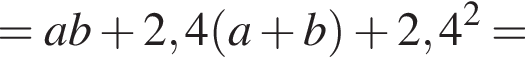
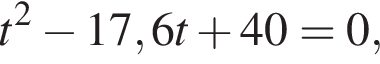 поэтому равны
поэтому равны 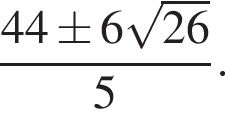
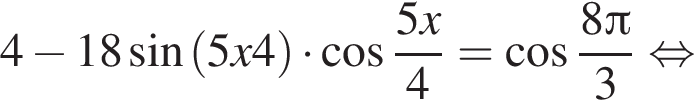
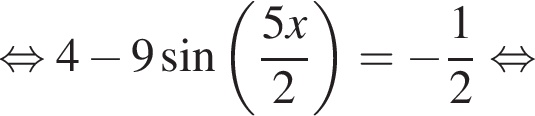
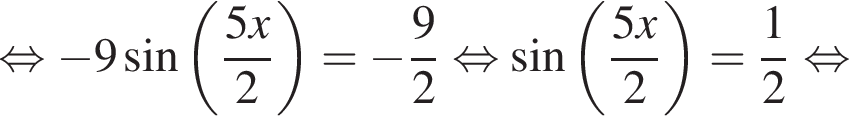
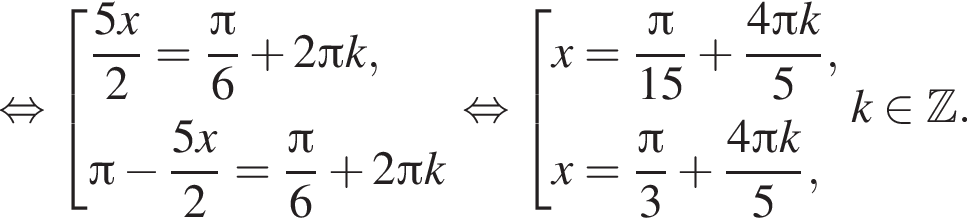
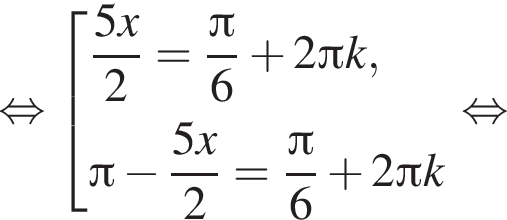
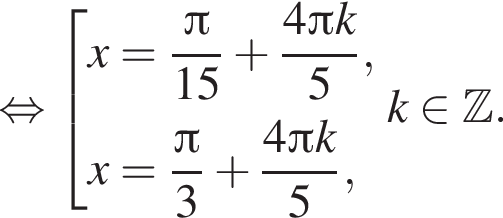
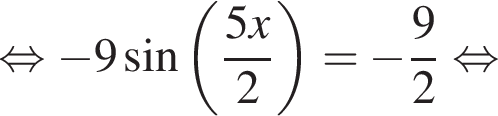
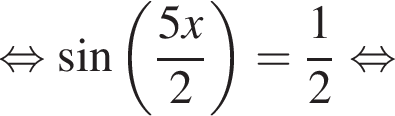
 Поскольку
Поскольку 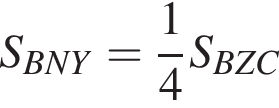 (NY — средняя линия), поэтому
(NY — средняя линия), поэтому 
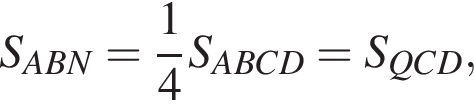 тогда
тогда 

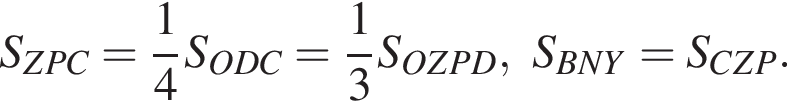
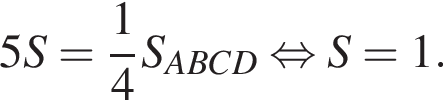
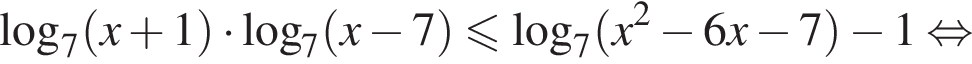
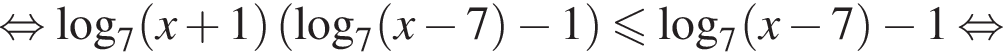
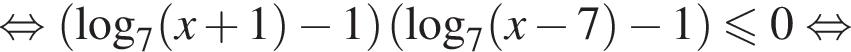
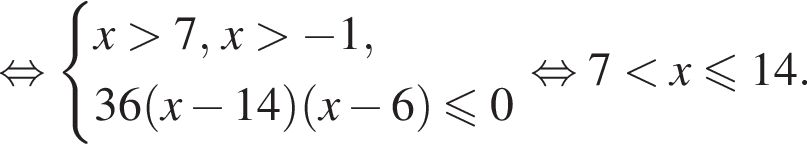

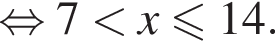
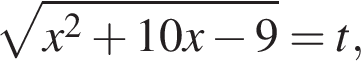 тогда
тогда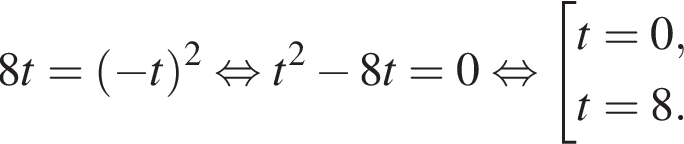
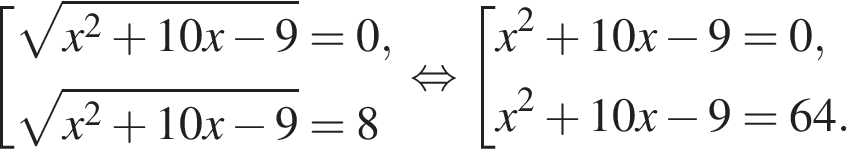
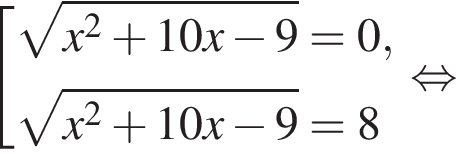
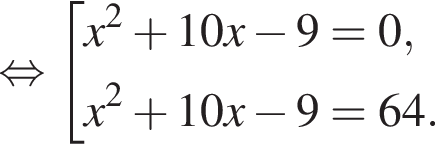
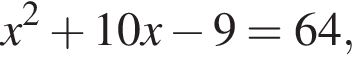 то
то 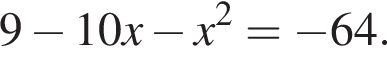 Подставив полученные числа в исходное уравнение, получим:
Подставив полученные числа в исходное уравнение, получим: 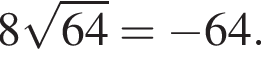 Следовательно, корни второго уравнения не являются решением. Решим первое уравнение и получим два решения:
Следовательно, корни второго уравнения не являются решением. Решим первое уравнение и получим два решения: 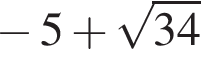 и
и 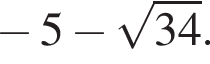
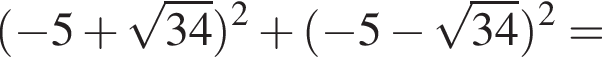
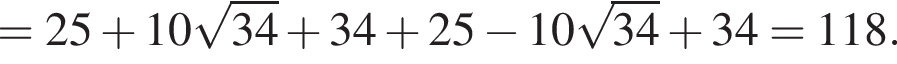
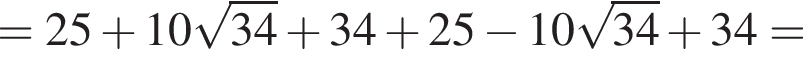
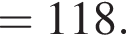
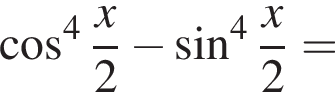
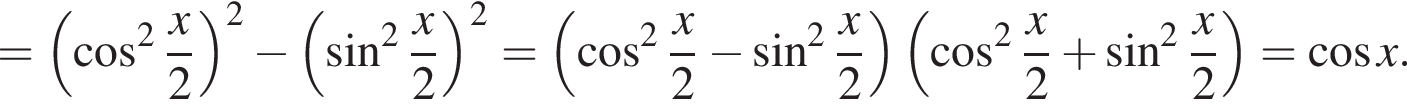
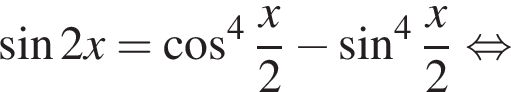
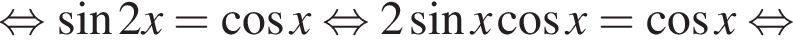
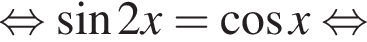

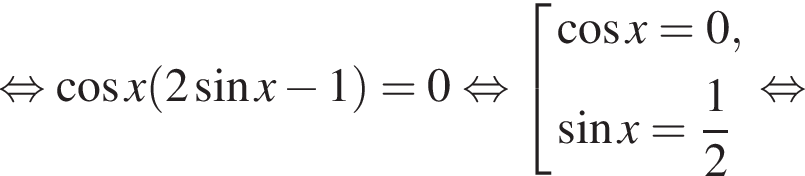
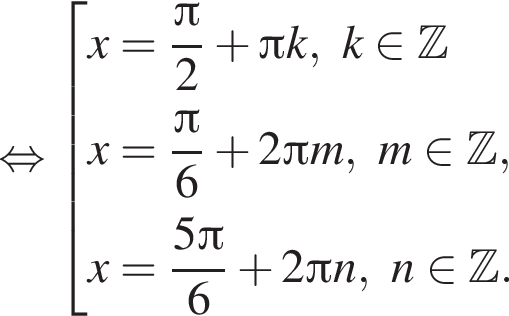
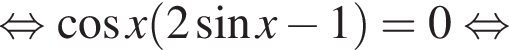
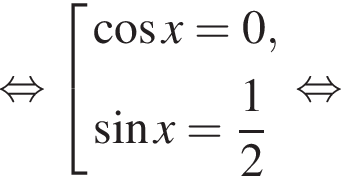
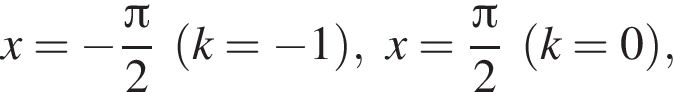
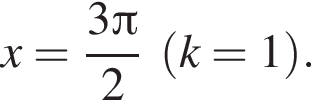 Их сумма равна
Их сумма равна 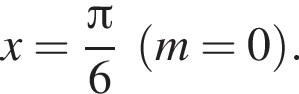 Их сумма равна
Их сумма равна 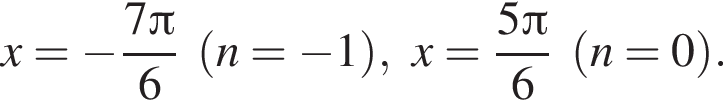 Их сумма равна
Их сумма равна 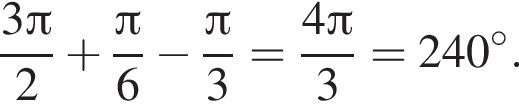
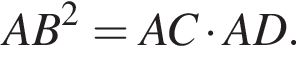 Обозначим AB за x, тогда
Обозначим AB за x, тогда  Тогда:
Тогда: 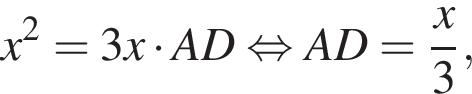 при этом
при этом 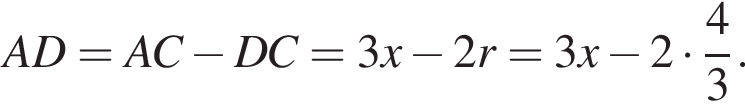 Получим:
Получим: 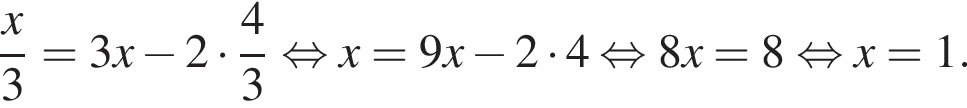
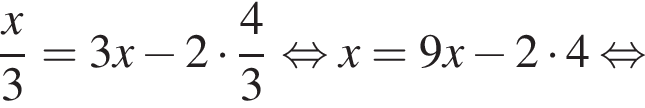
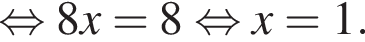
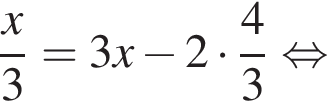
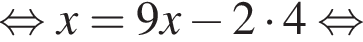
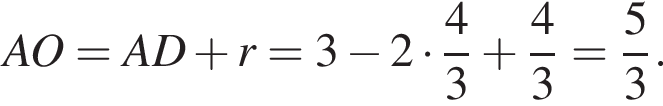
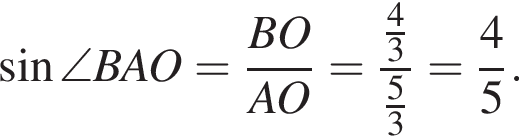 Тогда площадь треугольника ABC:
Тогда площадь треугольника ABC: 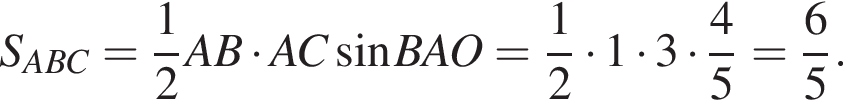
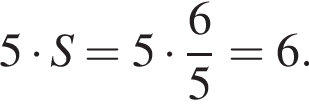
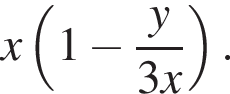 Второй работал
Второй работал 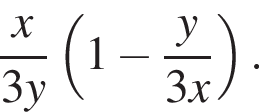 Если оба они выполнили
Если оба они выполнили 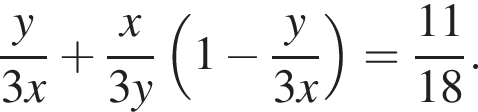 Пусть
Пусть 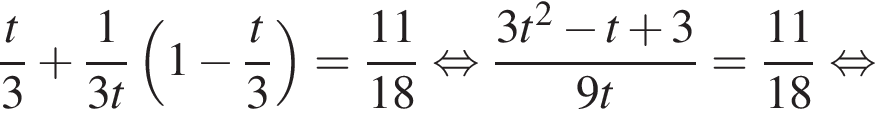
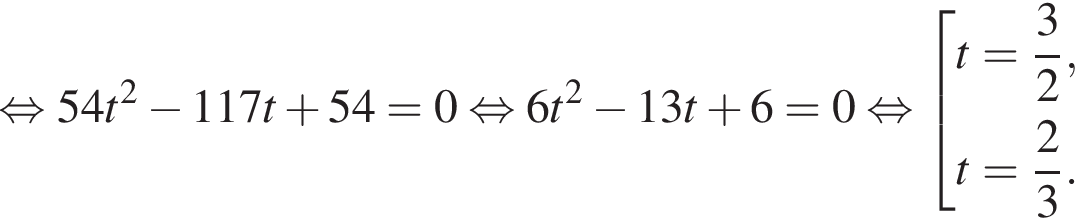

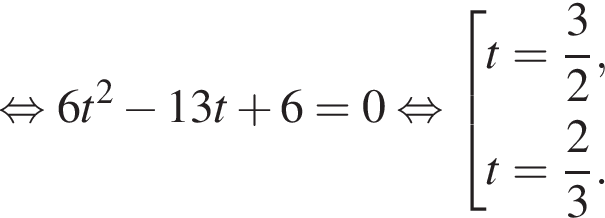
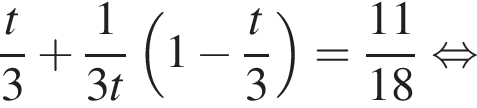
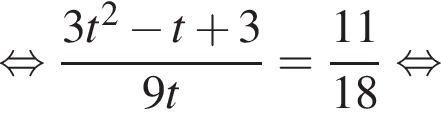
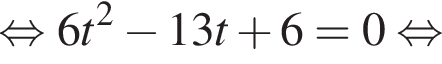
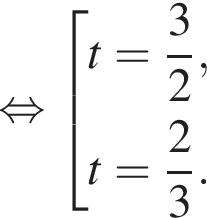
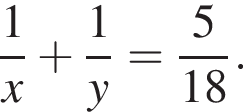 Зная, что
Зная, что 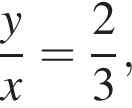 получаем, что x = 6, y = 9, или x = 9, y = 6. Таким образом, рабочему с меньшей производительностью потребуется 9 часов.
получаем, что x = 6, y = 9, или x = 9, y = 6. Таким образом, рабочему с меньшей производительностью потребуется 9 часов.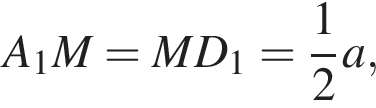
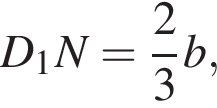
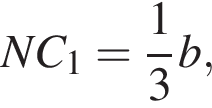
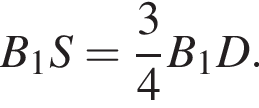
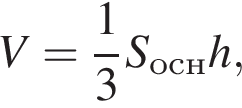 где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на втором рисунке.
где основание — KNC1B1. Проведем высоту SE из точки S пирамиды SB1KNC1, как показано на втором рисунке.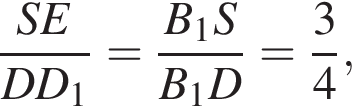 поэтому
поэтому 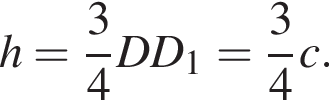



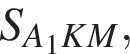 для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1 (см. рис. 3). Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому:
для этого сделаем дополнительное построение, проведя прямую параллельную B1M до пересечения с продолжением стороны A1D1 (см. рис. 3). Получившийся треугольник D1NF подобен треугольнику A1B1M по двум углам. Поэтому: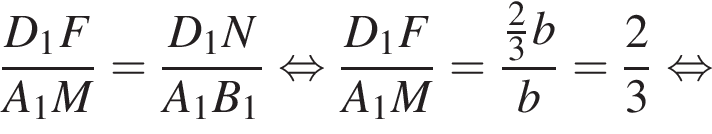
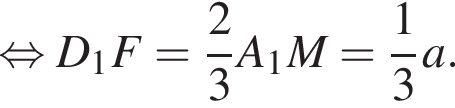

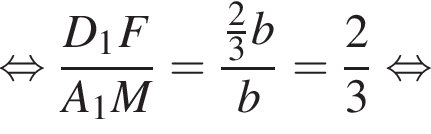
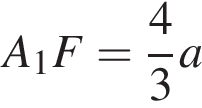 и
и 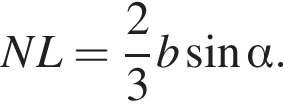 Соответственно, площадь треугольника A1NF равна
Соответственно, площадь треугольника A1NF равна 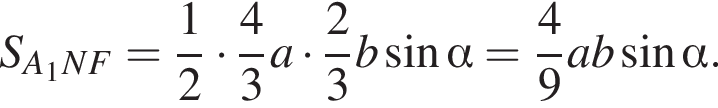
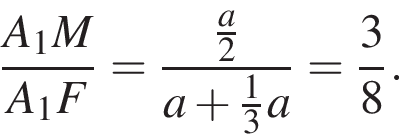
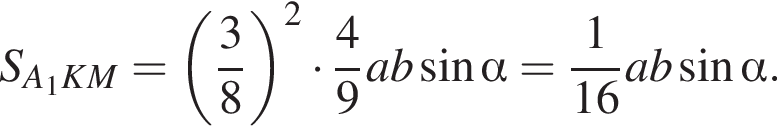
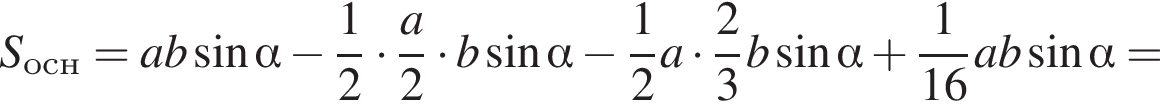
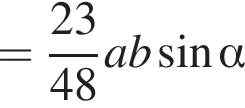

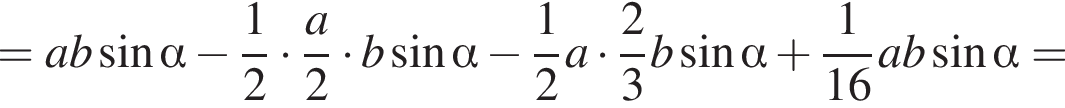
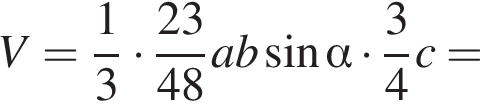
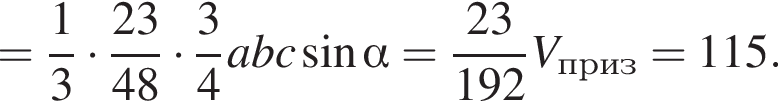
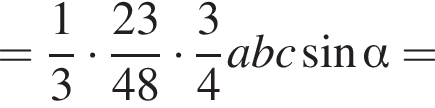
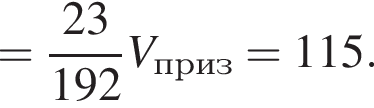
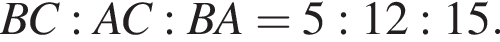 По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 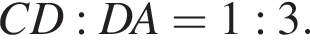 Значит, если
Значит, если  то
то 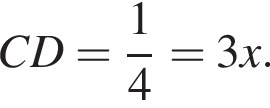
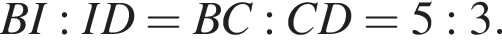 Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что 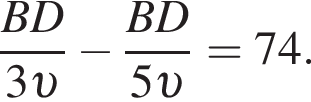
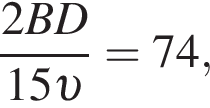 откуда
откуда 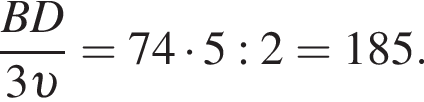
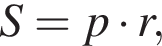 где p — полупериметр. Находим:
где p — полупериметр. Находим: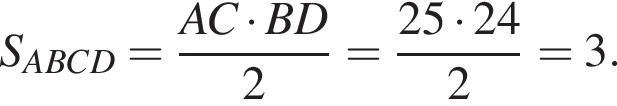
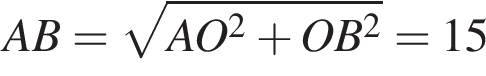 и
и 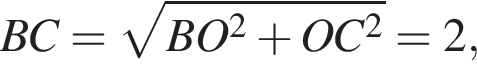 следовательно,
следовательно, 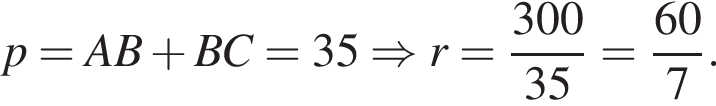
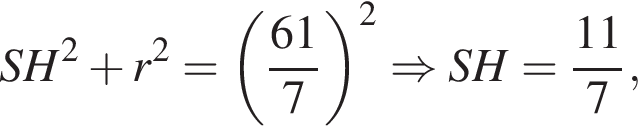
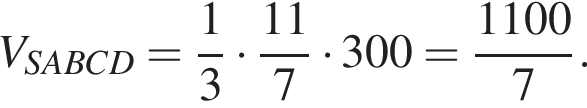
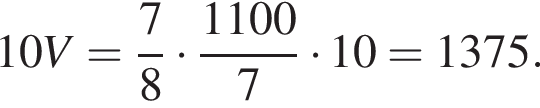
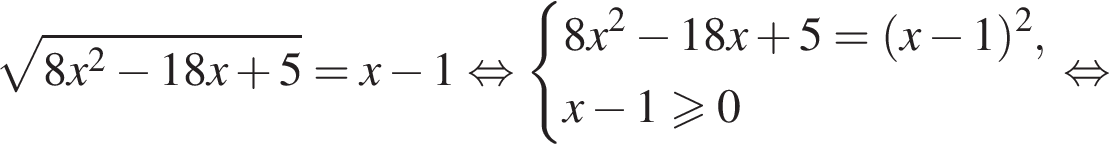
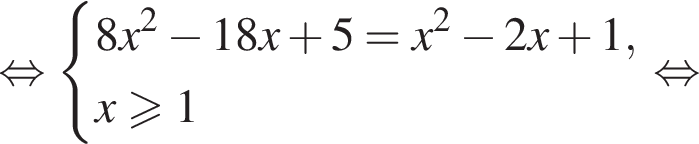
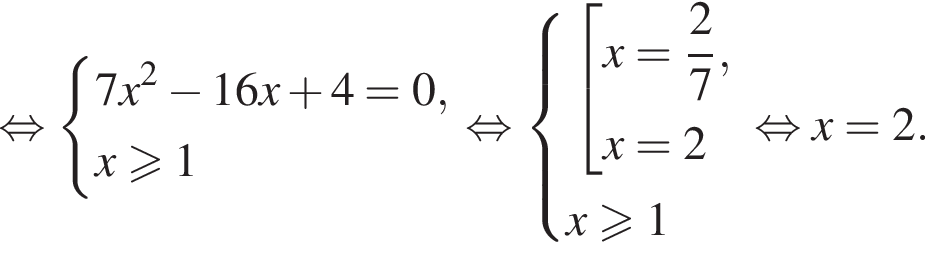
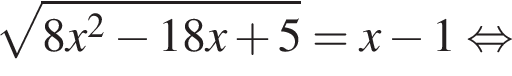
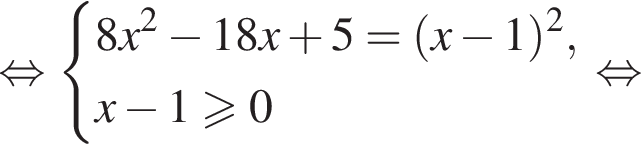
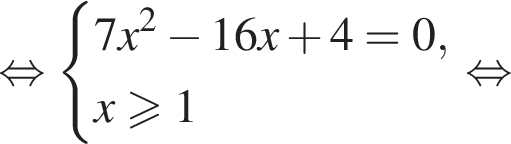
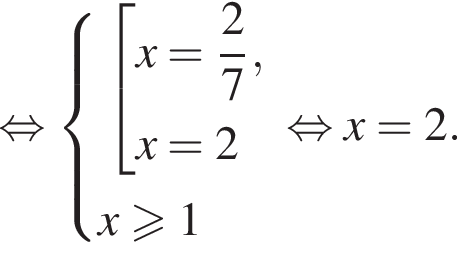
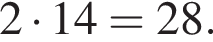
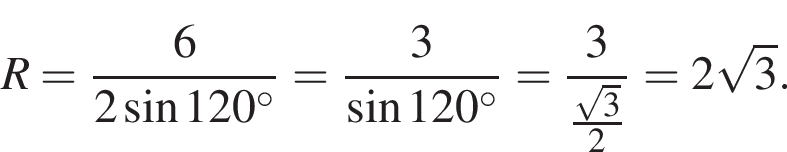
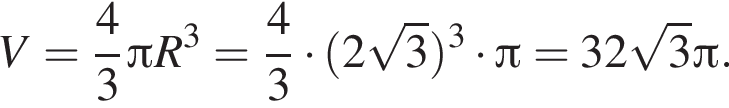
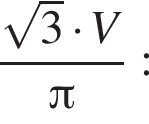
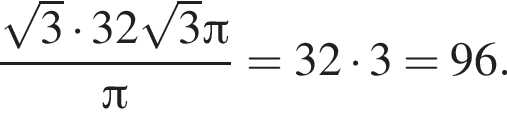
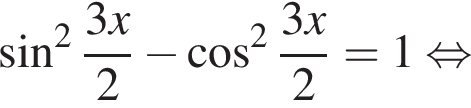
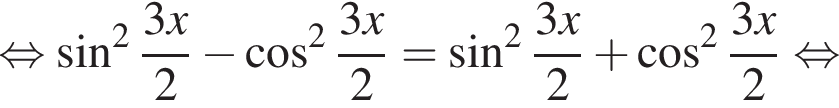
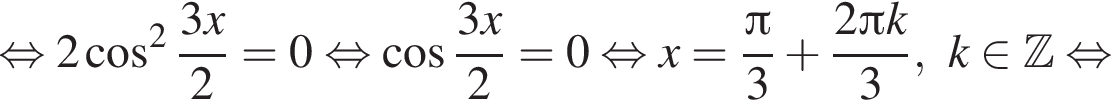
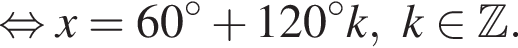
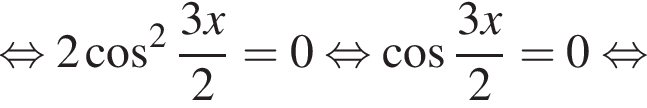
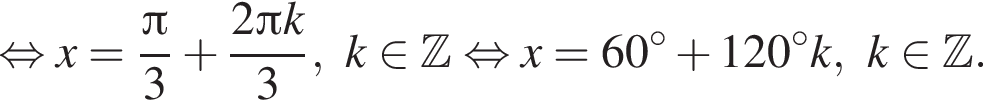
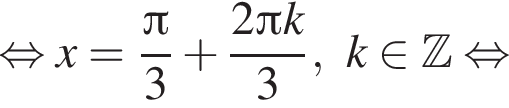
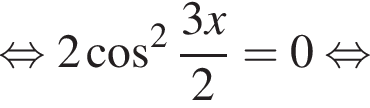
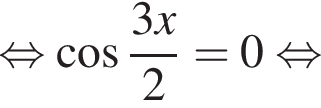
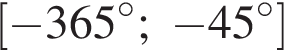 удовлетворяют решения x = −60°, x = −180°, x = −300°, сумма этих корней равна −540°.
удовлетворяют решения x = −60°, x = −180°, x = −300°, сумма этих корней равна −540°.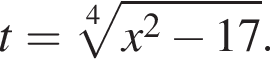 Тогда:
Тогда:
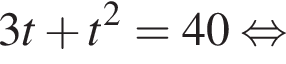
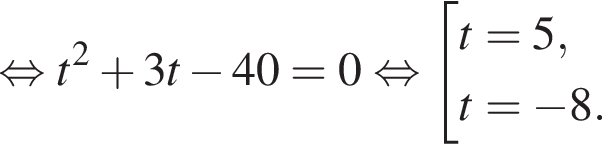
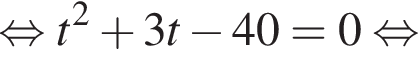
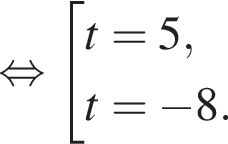
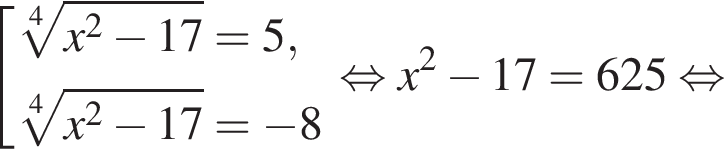
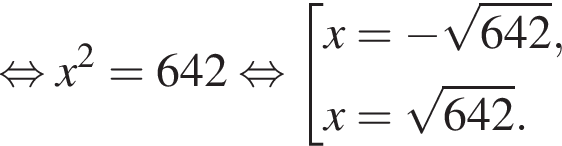
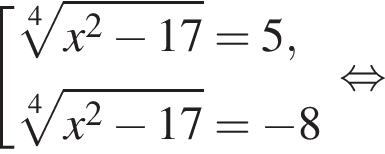
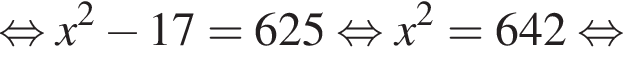
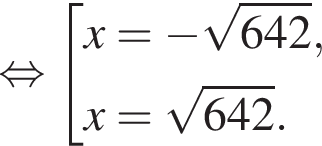
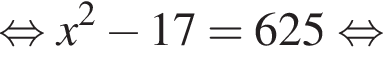

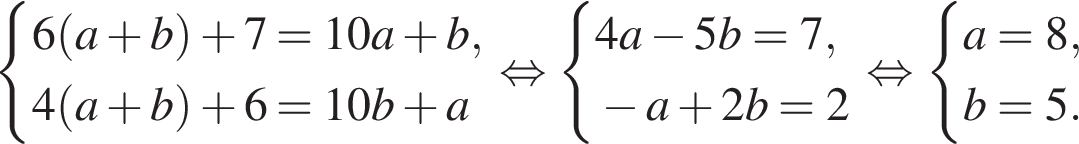
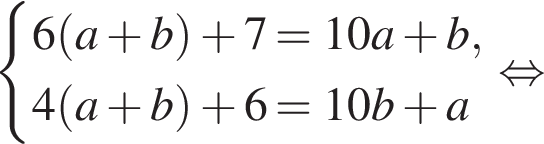
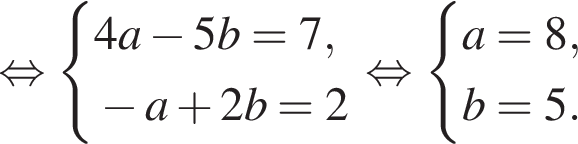
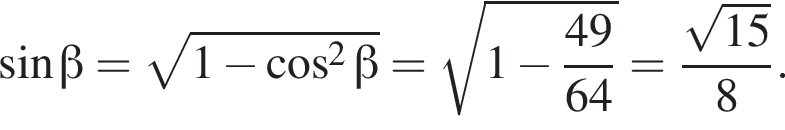
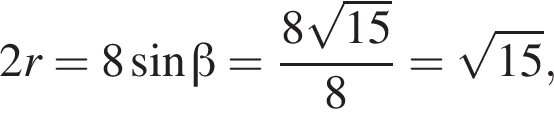
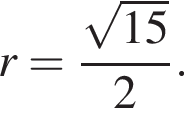 Тангенс угла α равен отношению высоты пирамиды к радиусу окружности, вписанной в ромб. Имеем:
Тангенс угла α равен отношению высоты пирамиды к радиусу окружности, вписанной в ромб. Имеем: